Research
Architecture By Tetris Puzzle
Enumeration of Shape CompositionsUniversity of Kansas
2025

This project explores the combinatorial possibilities of placing a T-shaped piece and an L-shaped piece—two of the most recognizable forms from the Tetris puzzle—within the confines of a 4×4 square grid. The task begins with a systematic enumeration of all possible configurations where the two pieces can fit without overlap, covering the spatial logic of adjacency, rotation, and orientation. Each placement yields a different composition, with the total number of distinct arrangements calculated at 148 before any reduction. However, not all of these are fundamentally unique, as many are merely reflections or rotations of others. By applying symmetry elimination—removing duplicates that are equivalent under rotation (90°, 180°, 270°) or reflection across the vertical, horizontal, and diagonal axes—the final set is distilled to 24 unique compositions. These 24 results are particularly meaningful, because they represent the core design vocabulary generated from two simple shapes under strict constraints. Beyond a combinatorial puzzle, the study suggests architectural potential: each composition can be read as a miniature building form, where the T-piece represents a T-shaped wall and the L-piece represents an L-shaped wall. Together, they define interior and exterior space, circulation paths, and relationships between volumes. In this way, the abstract exercise becomes a tool for architectural imagination, compressing complex ideas of structure and space into compact, rule-based diagrams. The project demonstrates how design can emerge not only from the continuous manipulation of form, but also from discrete and rigorous exploration of limited elements within bounded conditions. Just as Tetris itself is a game of constraint and fit, the compositions derived here show how playful geometry can open unexpected avenues in spatial design. The final collection of 24 unique configurations offers a catalog of small architectures that embody both mathematical precision and creative expression.
![]()
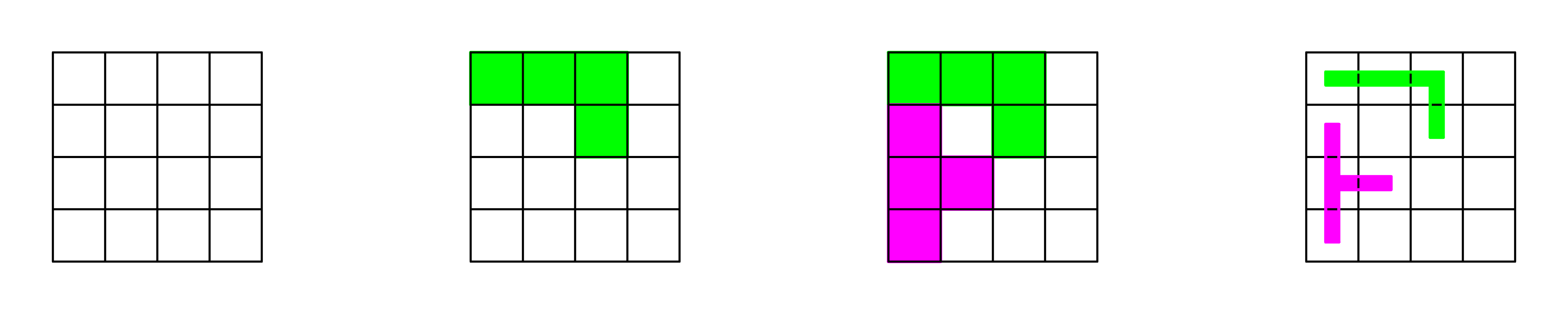
24 unique compositions (124 symmetrical copies are removed)

Mapping to 3X3 Square-grid with line representation

Before reduction, 148 compositions in 24 groups:

52 ways to place a T-shape piece in an irregular board
