Research

Revisit Alberti

Implementing Two-Point Perspective Transformation in DrawScript

University of Kansas
2024


Spencer JR (1956)

Nowadays, the algorithms of implementing perspectival transformations including one-point and two-point perspectival transformations are critical in computer-aided design (CAD) since CAD applications are to represent 3D objects on a two-dimensional display. The most common algorithm is to adopt linear transformation matrices to algebraically calculate the coordinates (Hong 2022). The algorithm of linear transformation matrices is fast and efficient and broadly used in current CAD applications. However, algebraic calculations involve in rounding errors, especially in perspective transformations because the derivation of perspective transformation is involved in high-degree linear equations (Hong and Economou 2023).  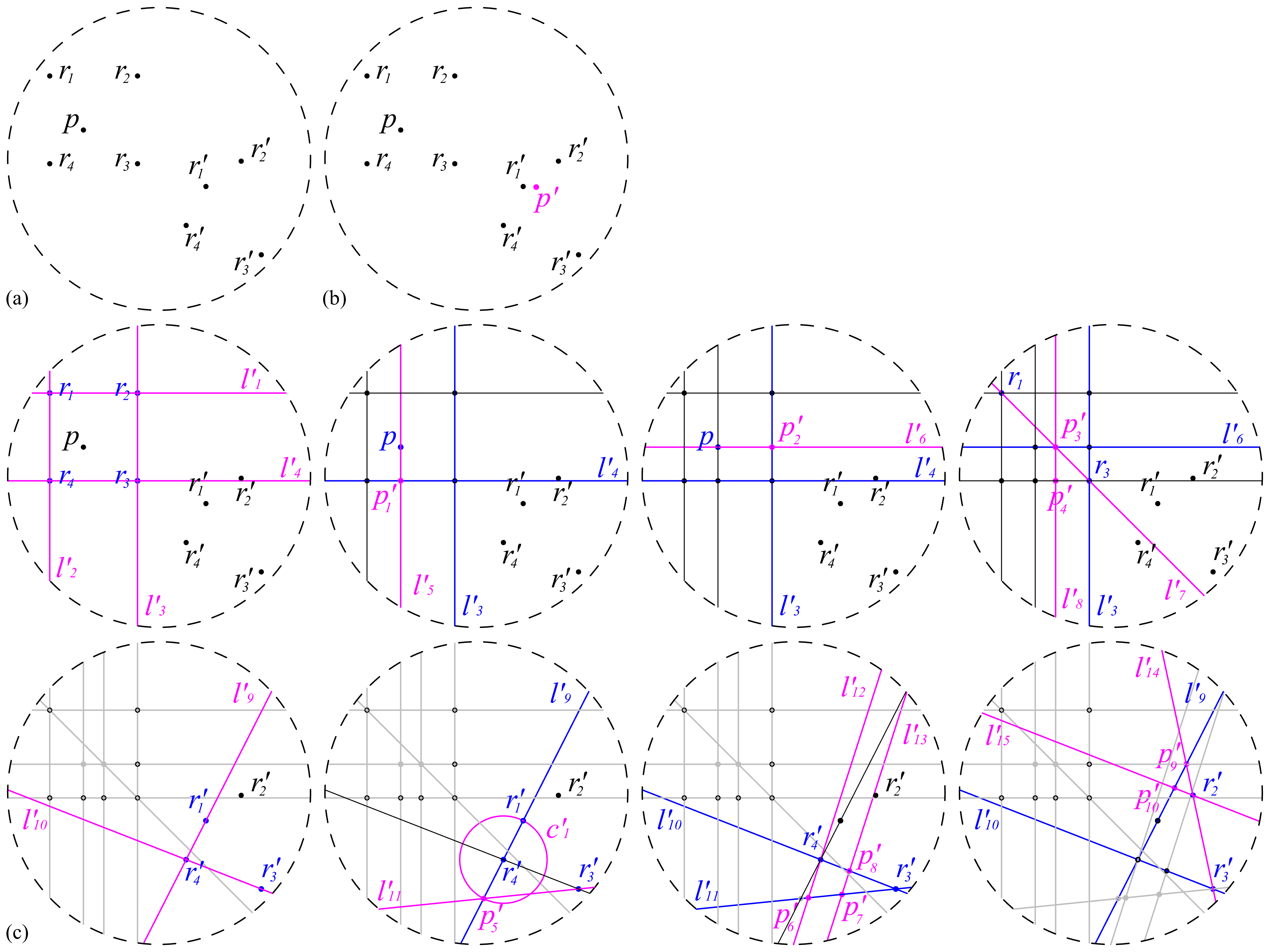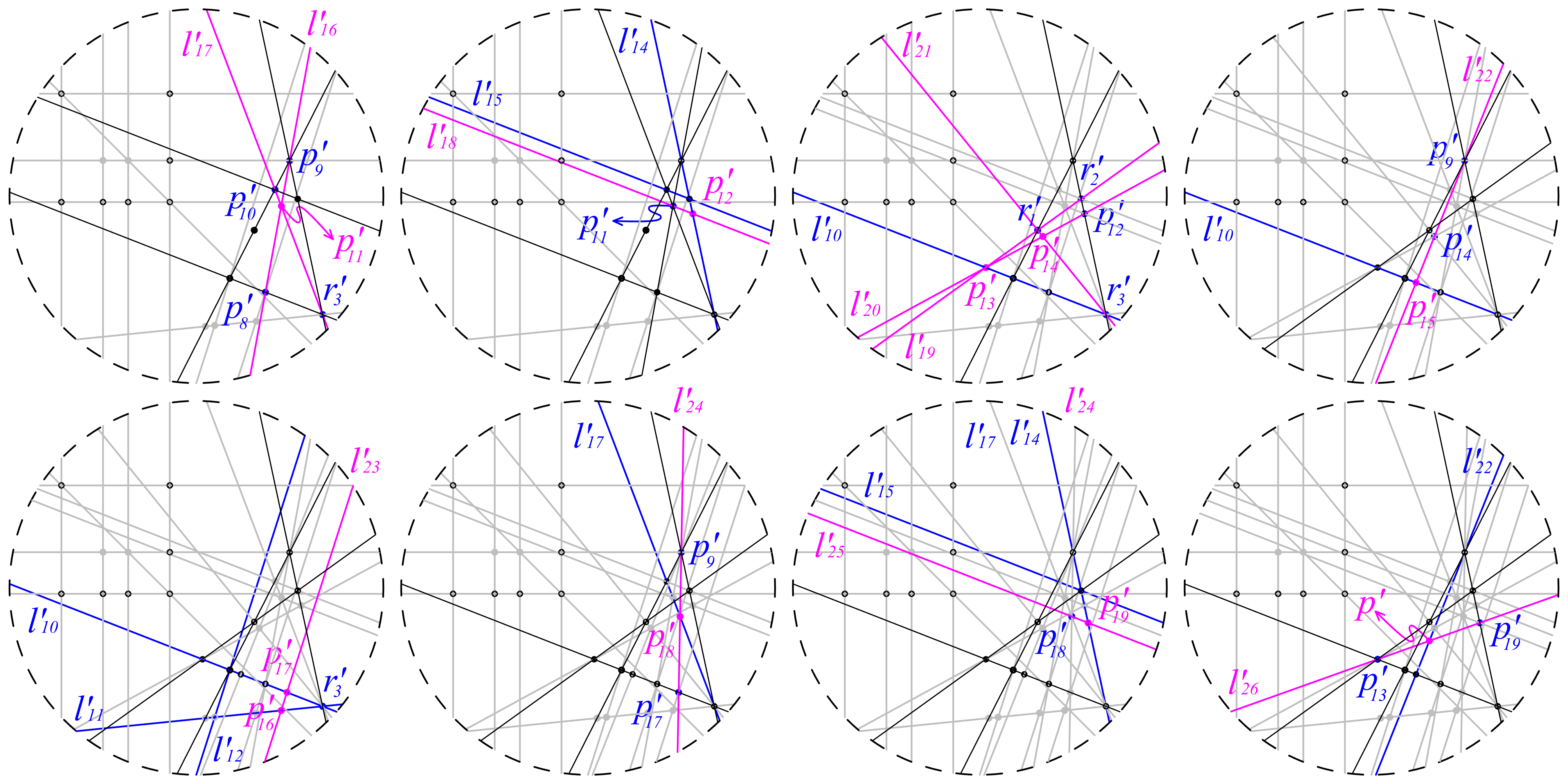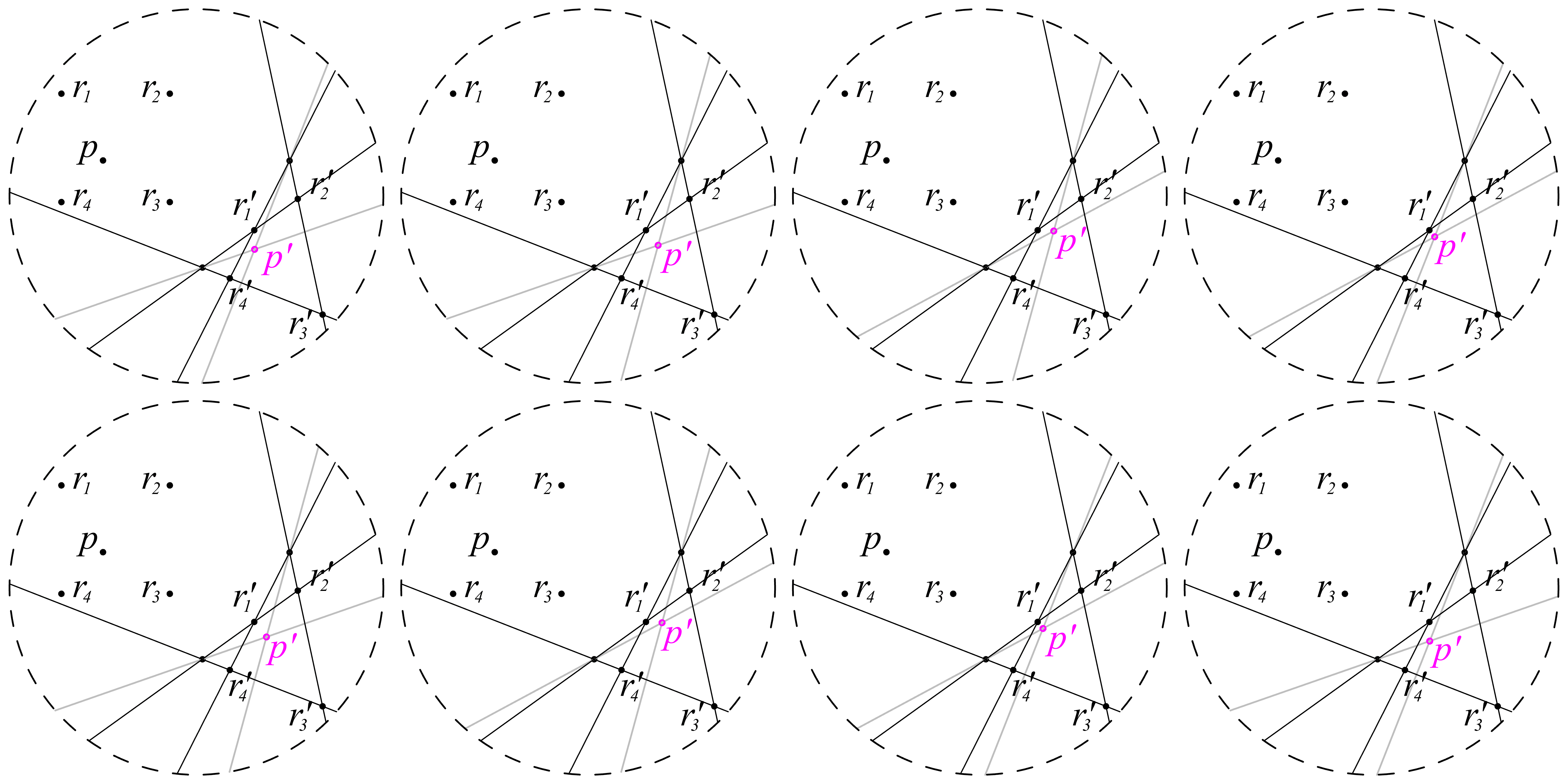By revisiting Alberti’s geometric constructions (Alberti 1450; 1956) which implement a perspectival transformation on a planar plane, it is a fascinating idea that perspectival transformation can be derived without algebraic calculation. Moreover, a precedent study by Dr. Ramesh Krishnamurti (2015) is foundation of this work, where he proposed an alternative representation system to avoid infinite numbers and irrational numbers. For instance, an irrational number √2 can be represented with a sequence of geometric constructions of a diagonal line of a 1X1 square, instead of representing its numerical value. Nevertheless, the implementation of automatic geometric constructions in computer is tricky since geometric constructions in the end are still represented and implemented in numbers and symbols because the symbolic programming languages such as Python, C++, C# and so forth, are the most accessible media to implement geometric constructions in computer, which increase much complexity in implementation Study here picks up this idea and implement geometric constructions in DrawScript, a visual programming language which allows to compute shapes directly, to replace algebraic calculation for implementing perspectival transformation, meanwhile avoiding the complexity of symbolic implementation. In total, there are 253 lines of DrawScript codes used for implementing perspectival transformation.



Demo Video on Youtube:
Revisit Alberti